GEOMETRIA PLANA

Introducción

La geometría plana es una rama de geometría dedicada al estudio de las figuras bidimensionales, es decir, aquellas que se grafican en un plano. La geometría plana analiza elementos como unidimensionales como la recta, la semirrecta y el segmento. De igual modo, forman parte de este campo de estudios los ángulos y los polígonos.

Esta rama de geometría implica muchas veces la simplificación del mundo que nos rodea en un plano, de manera que no pueden estudiarse todas las características de los objetos. Por ejemplo, no se podría analizar todas las dimensiones de una caja, sino cada una de sus caras que son cuadriláteros.

La geometría plana tiene sus orígenes en la antigüedad, siendo su principal antecedente la obra Los Elementos del matemático griego Euclides y que data del siglo IV A.C. Este es considerado como uno de los textos más influyentes de la historia y recopila nociones básicas de elementos como rectas y polígonos, e incluso podemos encontrar el famoso teorema de Pitágoras.

Elementos de la geometría plana

Los elementos que estudia la geometría plana son:

  • Recta: Es un elemento unidimensional constituido por una serie infinita de puntos que van a una sola dirección, es decir, no presenta curvas.

  • Semirrecta: Al igual que la recta, es un elemento unidimensional que consiste en una secuencia de puntos, pero no es indefinida, sino que tiene un origen y se prolonga al infinito. Puede definirse también como la porción de una recta definida a partir de un punto de corte.

  • Segmento: Es un elemento unidimensional constituido puntos que van en una sola dirección, pero , a diferencia de la semirrecta, está acotado por un punto de origen y un final.




  • Ángulo: Es el arco que se forma a partir del cruce u origen de dos elementos bidimensionales, ya sean rectas, semirrectas o segmentos.



  • Polígono: Es una figura bidimensional formada por una serie finita de segmentos no colineales (no forman parte de la misma recta), de manera que forman un espacio cerrados. Algunos ejemplos son los cuadrados, los rectángulos, los rombos, los triángulos o los octógonos. Los polígonos pueden clasificarse en:
    • Regulares: Cuando todos sus lados y ángulos interiores tienen la misma medida.
    • Irregulares: Cuando no todos sus lados y ángulos interiores son idénticos.





  • Circunferencia: Es una figura geométrica plana y cerrada que se caracteriza porque todos los puntos que la constituyen se ubican a la misma distancia del centro. Dicha distancia constante se llama radio. También se define a la circunferencia como el perímetro del círculo.



Bibliografía:


Ángulos

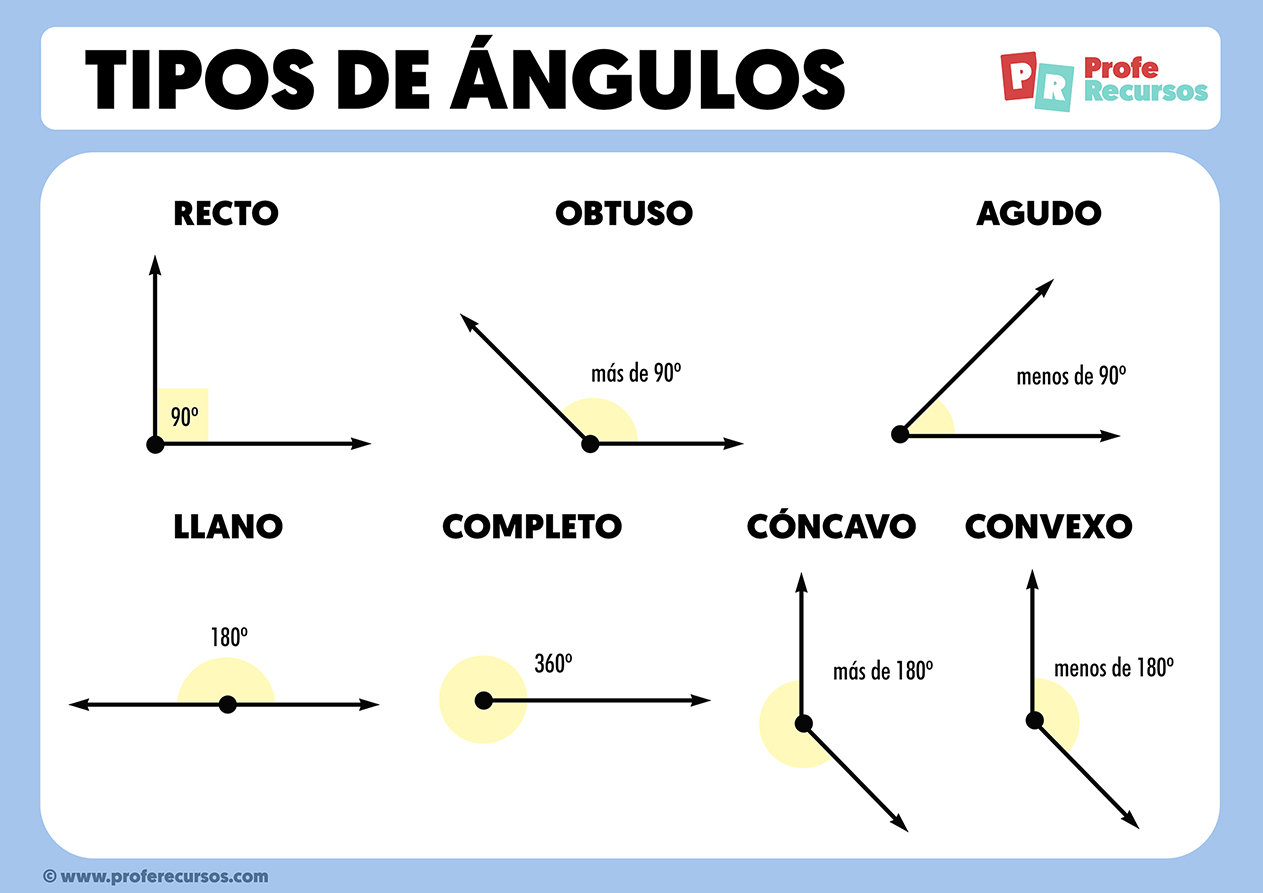
Tipos de ángulos por su suma:

  • Complementarios
  • Suplementarios

Decimos que dos ángulos son complementarios si su suma forma un ángulo recto, es decir, 90º.

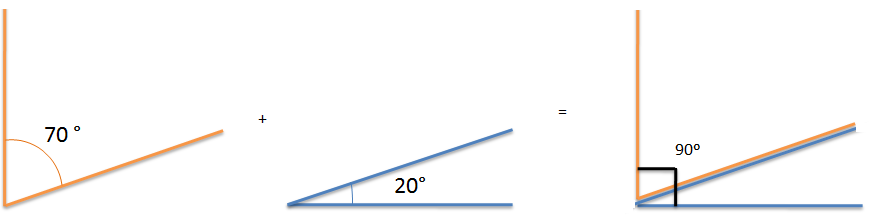
Con esta imagen vemos que la suma de los ángulos de 70° y de 20° es 90°.

 

En este caso 70 ° y 20 ° son complementarios porque 70° + 20° = 90°.

Más ejemplos podrían ser 47° y 43°, ya que 47° + 43° = 90°, 30° y 60°,  45° y 45° , etc.

Dos ángulos son suplementarios si su suma forma un ángulo llano, es decir, 180°.

En esta imagen tenemos los ángulos de 160° y de 20°. Los dos lados suman un ángulo llano, 180°.

160° y 20° son suplementarios porque suman 180°.

110° y 70° también lo son ya que 110° + 70° = 180°, lo mismo para 25° y 155°.

Tipos de ángulos por su posición:

  • Consecutivos
  • Adyacentes
  • Opuestos por el vértice

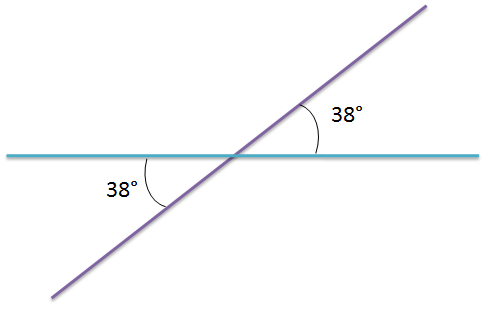
Los ángulos que tienen el vértice y un lado común se llaman ángulos consecutivos.

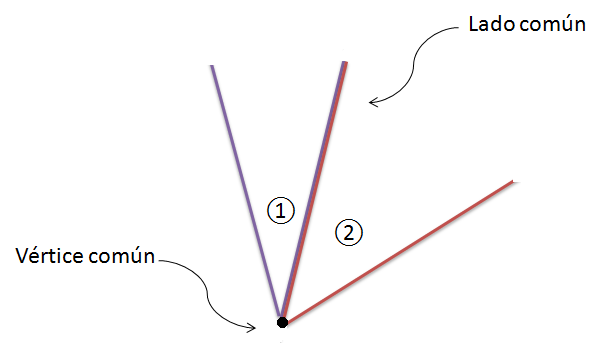
Los ángulos ① y ② son consecutivos ya que comparten el vértice y uno de los lados como podéis observar en la imagen.

Dos ángulos adyacentes tienen en común el vértice y uno de los lados, es decir son consecutivos, pero a la vez la suma de éstos tiene que ser de 180°, suplementarios.

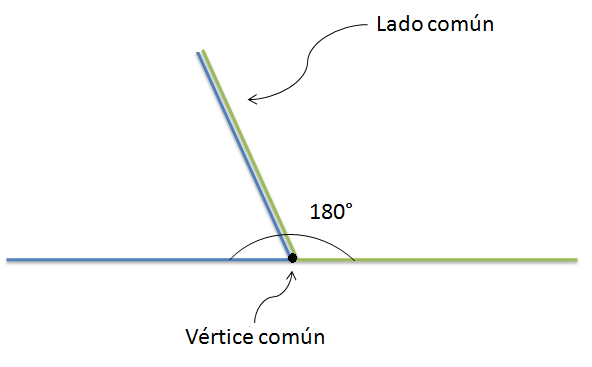
Se muestran dos ángulos adyacentes ya que además de compartir el mismo vértice y un lado, la suma de los dos ángulos es de 180°.

Dos ángulos opuestos por el vértice tienen el vértice común y sus lados son semirrectas opuestas. Siempre tienen igual medida, ya que tienen la misma amplitud.

¡Ya sabes los tipos de ángulos que hay según su suma y su posición!

Bibliografía:

https://www.smartick.es/blog/matematicas/geometria/angulos-tipos-suma-posicion/

https://www.smartick.es/blog/matematicas/geometria/angulos-consecutivos/

https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/clasificacion-de-angulos.html

https://www.disfrutalasmatematicas.com/geometria/angulos.html


Características de los Triángulos

Vamos a estudiar qué es un triángulo y las diferentes formas de clasificarlo. Empezaremos diciendo que un triángulo es un polígono que tiene tres lados. También podemos definirlo como el área cerrada por tres rectas. Además de tener tres lados, un triángulo también tiene tres ángulos y tres vértices. Veámos qué es cada uno de ellos:

  • TRIÁNGULO:
    • Lados: tiene tres y son las rectas que forman el polígono.
    • Vértices: tiene tres y son cada uno de los puntos donde se unen dos lados.
    • Ángulos: tiene tres y son las aberturas que se forman al unirse dos lados.

Habitualmente los lados de los triángulos suelen representarse con letras minúsculas de la «a» a la «c» mientras que los ángulos siguen la misma nomenclatura solo que en mayúsculas. La imagen siguiente te ayudará mejor a comprender esto:

Tipos de triángulos

Los triángulos son los polígonos más sencillos, pero son de gran ayuda para el estudio de las propiedades de otros polígonos más complejos, como por ejemplo, para estudiar sus áreas.

Tipos de triángulos

 

Antes de empezar a ver los diferentes tipos de triángulos que hay debemos decir que éstos se clasifican según la medida de sus lados o la amplitud de sus ángulos. Un esquema de esto podría ser:

  • Tipos de triángulos
    • Clasificación de triángulos según lados:
      • Triángulo equilátero
      • Triángulo isósceles
      • Triángulo escaleno
    • Clasificación de triángulos según sus ángulos:
        • Triángulo rectángulo
        • Triángulo acutángulo
      • Triángulo obtusángulo

Veamos ahora uno por uno:

Clasificación de triángulos según sus lados

Existen tres tipos de triángulos según sus lados que son:

  • Triángulo equilátero:
    • Tiene sus tres lados iguales, es decir, los tres lados son de la misma longitud.
  • Triángulo isósceles:
    • Tiene dos lados iguales (de igual longitud) y otro no.
  • Triángulo escaleno:
    • Tiene los tres lados diferentes, es decir, de distinta longitud.
Bibliografía:

Rectas

1. Introducción


Recordad que la ecuación de una recta es

Explicamos cuándo dos rectas son paralelas o perpendiculares atendiendo a su pendiente. Con ejemplos y problemas resueltos paso a paso. ESO. Secundaria. Geometría plana. Matemáticas.

El coeficiente � es la pendiente y � es la ordenada en el origen.

El valor de la pendiente, �, es la causa de un mayor o menor crecimiento.

Ejemplo 1

La recta �=2�+1 crece más rápido que �=�+1 porque tiene una pendiente mayor:

Explicamos cuándo dos rectas son paralelas o perpendiculares atendiendo a su pendiente. Con ejemplos y problemas resueltos paso a paso. ESO. Secundaria. Geometría plana. Matemáticas.


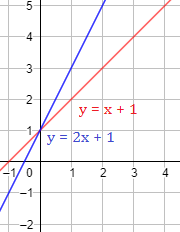
El valor de la ordenada en el origen, �, es la segunda coordenada del punto de corte de la recta con el eje Y.

Ejemplo 2

La recta �=2�+1 corta al eje Y en (0,1) y la recta �=�+2 lo hace en el punto (0,2):

Explicamos cuándo dos rectas son paralelas o perpendiculares atendiendo a su pendiente. Con ejemplos y problemas resueltos paso a paso. ESO. Secundaria. Geometría plana. Matemáticas.


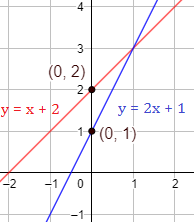
2. Paralelas


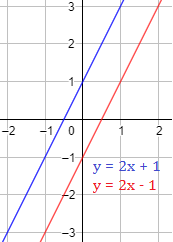
Dos rectas son paralelas cuando no se cortan. Esto ocurre cuando las rectas tienen la misma pendiente.

Ejemplo 3

Las rectas �=2�+1 e �=2�−1 son paralelas. Observad que tienen la misma pendiente, �=2:

Explicamos cuándo dos rectas son paralelas o perpendiculares atendiendo a su pendiente. Con ejemplos y problemas resueltos paso a paso. ESO. Secundaria. Geometría plana. Matemáticas.


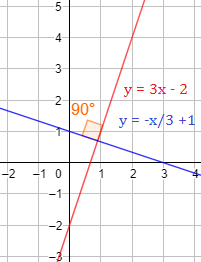
3. Perpendiculares

Dos rectas son perpendiculares cuando se cortan formando un ángulo recto (ángulo de 45°).

Esto ocurre cuando la pendiente de una de las rectas es el opuesto del inverso de la otra. Es decir, si la pendiente de una de las rectas es �, la otra debe ser −1/�.

Ejemplo 4

Las rectas �=3�−2 e �=−�/3+1 son perpendiculares:

Explicamos cuándo dos rectas son paralelas o perpendiculares atendiendo a su pendiente. Con ejemplos y problemas resueltos paso a paso. ESO. Secundaria. Geometría plana. Matemáticas.

Bibliografía:

https://content.nroc.org/DevelopmentalMath/TEXTGROUP-9-14_RESOURCE/U13_L2_T3_text_final_es.html

https://www.superprof.es/apuntes/escolar/matematicas/analitica/recta/rectas-paralelas-y-perpendiculares.html

https://www.matesfacil.com/ESO/geometria_plana/paralelas/problemas-resueltos-rectas-paralelas-perpendiculares-pendiente-puntos.html

https://www.problemasyecuaciones.com/geometria2D/paralelas-perpendiculares/rectas-paralelas-perpendiculares-ejemplos-problemas-resueltos.html

https://www.neurochispas.com/wiki/rectas-paralelas-y-perpendiculares-formulas-y-ejemplos/